Approximate Tree Embedding

According to the XML Information Set W3C Recommendation [1], XML documents can be represented as trees. Complex queries can also be represented as pattern trees to be searched in the documents.

Finding structural approximate answers to complex queries, i.e. queries with two or more branching conditions, is known to be a hard task task, namely, finding a solution to the Unordered Tree Embedding Problem, which is proved to be NP-complete [2].

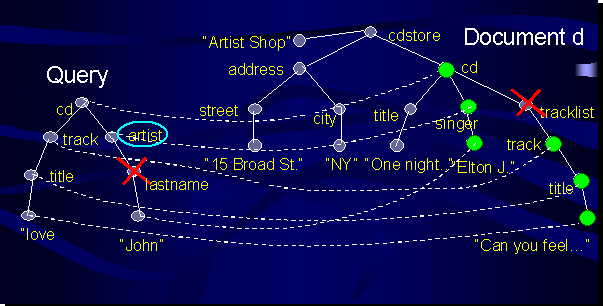
Consider the approximations shown in Figure 2:

Figure 2: Approximate Tree Embedding of the query tree in the document tree.

The semantic condition on artist is relaxed to match to the synonym singer, the

lastname element is disregarded thus accepting a partial match of the query, and

finally the tracklist element is skipped in the data.

We recall that, given two trees t₁ and t₂, an injective function f from nodes of t₁ to nodes of t₂ is an Embedding of t₁ in t₂ if it preserves labels, and ancestorships in both directions [2].

In order to cope with the intrinsic complexity of the problem, and make the embedding function efficiently computable, we guarantee ancestorship only in one direction, from query tree to document tree. This means that injectivity is not guaranteed by the mapping, in that sibling nodes in the query may be mapped to ancestor-descendant nodes in the data.

Finally, approximations are captured by the following definition, which formulates the (one-way) Approximate Tree Embedding function:

Given two trees t₁ and t₂, a function e from nodes of t₁ to nodes of t₂ is an Approximate Embedding of t₁ in t₂ if:

1. e is a partial function                                                                     (node deletion)
2. For all q_i in dom(e), sim(label(q_i),label(e(q_i)))>0                             (node renaming)
3. For all q_i, q_j in dom(e), parent(q_i,q_j) => ancestor(e(q_i),e(q_j))           (node insertion)

where sim is a similarity function between labels of nodes, possibly exploiting thesauri, ontologies, and semantic networks; parent and ancestor are the usual hierarchical relationships between nodes.

[1]  XML Information Set. http://www.w3.org/TR/xml-infoset

[2]  P. Kilpeläinen. Tree Matching Problems with Application to Structured Text Databases. PhD. Thesis, Dept. of Computer Science, Univ. of Helsinki, SF, 1992.